Resumo

O incentivo à criação de conjecturas e justificativas formais por parte dos estudantes nas aulas de matemática tem sido negligenciado nos últimos anos, mesmo com os apelos dos Parâmetros Curriculares Nacionais e dos recentes resultados de pesquisa na área da Educação Matemática que atestam a importância de tais práticas na escola. Visando contribuir para uma mudança nesta situação, este artigo discute maneiras de retomar tais práticas no ambiente escolar, colocando as tecnologias digitais como ferramentas com potencial de transformação. Neste contexto, apresentam-se duas possiblidades de uso do computador: uma no campo geométrico e outra no campo numérico-algébrico.Nota-se que os ambientes computacionais os quais possuem representações dinamicamente conectadas, ferramentas de cálculo e de medidas podem fazer com que os estudantes realizem testes sistemáticos e percebam invariâncias, o que fomenta a formulação de conjecturas. Além disso, tais ambientes contribuem para que os estudantes abstraiam propriedades fundamentais na interação com o computador, o que pode ser a base de justificativas mais formais.

Palavras-chave: Conjectura, Prova, Computador, Educação Matemática.

ABSTRACT

Nowadays, the creation of conjectures and formal proofs by students in mathematics classroomshas been neglected, despite the recommendations of the National Curriculum and the recent research results in mathematics education that attest to the importance of such practices at school.In trying to change this situation, this article discusses ways to bring back such practices to the school environment considering the digital technologies as tools with potential for transformation. In this context, two possibilities of computer usehave been presented: one from the Geometric field and another from the Numeric-Algebraic field.As a conclusion, it is possible to see that technological environments that have dynamically connected representations, calculation and measure tools can make students to undertake systematic tests and notice invariance, which may foster the formulation of conjectures. In addition, these environments maycontribute to the students’ abstraction of fundamental properties that are important to write formal justifications.

Key-words: Conjecture, Proof, Computer, Mathematics Education

INTRODUÇÃO

A Matemática é uma área do conhecimento que se distingue das demais por dois motivos. O primeiro deles diz respeito ao caráter representacional de seus conceitos. Grande parte das ideias matemáticas não está presente fisicamente no mundo real e sua existência depende significativamente de representações simbólicas que foram desenvolvidas pela humanidade ao longo dos tempos. O segundo deles, diz respeito à validade e à aceitação dos conceitos, uma vez que as propriedades e relações entre eles são somente aceitas como verdadeiras pela comunidade matemática mediante à apresentação de uma justificativa redigida formal e logicamente. Estas justificativas formais são conhecidas na literatura da área como “prova” ou “demonstração”.

Reconhecer padrões, revelar a estrutura de um fenômeno numérico, métrico ou espacial, estabelecer relacionamentos, formular conjecturase prová-lasdedutivamente são atividades que regem a Matemática, a caracterizam como ciência e a destacam perante as demais.

A importância destas atividades para a Matemática como ciência influenciou o currículo escolar no Brasil e no mundo.Por volta dos anos 70-80, professores de matemática de diversos segmentos ensinavam teoremas dos mais variados para seus alunos e os forçavam a memorizar suas respectivas provas. Apesar de louvável, a tentativa de trazer um pouco do universo matemático para a sala de aula acabou em frustração. O trabalho,na escola, envolvendo conjecturas e provas matemáticas, ocorria de forma mecânica. Ao professor cabia escrever na lousa os principais teoremas acompanhados de uma infinidade de expressões simbólicas que, de alguma forma, atestavam a validade daquelas ideias. Ao aluno cabia copiar e decorar tudo para a hora da avaliação.

Ao reconhecer o pouco benefício que estas práticas traziam ao aluno, os professores foram pouco a pouco abandonando o trabalho com conjecturas e provas em suas salas de aula. Atualmente, poucos se preocupam em justificar formalmente as propriedades matemáticas que ensinam para seus alunos. Aqueles que se arriscam, validam as conjecturas utilizando casos provenientes do empirismo. Mais do que isto, o trabalho de formulação de hipóteses e o reconhecimento de padrões e estruturas têm sido negligenciados em detrimento do ensino de uma matemática repleta de regras e procedimentos os quais muitas vezes parecem desconectados.

Como professora e pesquisadora, tenho me incomodado profundamente com a situação de abandono ao trabalho com conjecturas e provas na escola, nestes últimos tempos. Na tentativa de superar esta situação, passei a estudar maneiras de resgatar essa prática, trazendo-a novamente para a sala de aula brasileira. Neste contexto, percebi as potencialidades que as tecnologias digitais, mais precisamente o computador, podem oferecer quando utilizadas significativamente pelo professor. Foi para descrever estas potencialidades e apresentar sugestões que redigi este artigo. Meu objetivo aqui é o de discutir a situação brasileira e internacional no que se refere ao trabalho com a formulação de conjecturas e provas na matemática escolar e apontar novas direções, tendo o computador como ferramenta com potencial de modificá-la positivamente.

AS CONJECTURAS E JUSTIFICATIVAS FORMAIS NA ESCOLA

Enquanto pesquisava a respeito da situação do ensino de conjecturas e provas na matemática escolar, vários questionamentos vieram a minha cabeça, tais como: prova é algo passível de ser ensinado da mesma forma que ensinamos frações, equações e conceitos geométricos? Se sim, existe alguma metodologia para seu ensino? Em que idade as pessoas devem aprender o que é uma prova? Quando podemos dizer que alguém sabe o que uma prova é? Se não, se prova é algo que não pode ser ensinado, como alguém aprende a provar? Existe alguma forma de torná-la algo ensinável? O primeiro passo na tentativa de buscar respostas para estas perguntas foi o de lembrar como aprendi a provar, em que circunstâncias e com que idade.

Lembrei que, durante toda minha fase como estudante da educação básica, nas aulas de matemática, meus professores exigiam que todos os alunos redigissem respostas completas para os exercícios propostos. Não bastava colocar somente um número na resposta. Havia necessidade de explicar como se chegou nela. Neste sentido, vejo que desde cedo a aula de matemática se configurou como um ambiente para que eu e meus colegas escrevessem justificativas. Entretanto, eu não me recordo de, durante a educação básica, ter engajado numa situação em que fosse necessário buscar justificativas para uma determinada conjectura matemática, criada ou não por mim.

Meu primeiro contato com a ideia de conjectura, demonstração e teorema ocorreu quando eu estava cursando matemática numa universidade. Eu estava na aula de fundamentos da álgebra e minha professora demonstrava na lousa diversos teoremas relativos à teoria dos números. Eu me recordo de conseguir acompanhar as explicações, mas de ter dificuldades de escrever minhas próprias provas. Eu aprendi a demonstrar observando o que minha professora produzia, comparando o que meus amigos escreviam com o que eu escrevia, e comparando como a professora avaliava o trabalho deles e o meu trabalho. Hoje, eu não sei dizer se minha professora tinha a intenção de nos ensinar como se demonstra teoremas ou não, ou se isso foi uma consequência do seu método de ensinar álgebra. O que eu sei é que, naquela época, eu descobri o que era uma prova porque eu estava inserida num ambiente em que elas eram usadas para explicar porque certas ideias da álgebra eram o que eram.

Já faz treze anos que passei por esta experiência e sempre me questiono se alguma coisa mudou nas salas de aula.
No Brasil, em 1998, foram publicados os Parâmetros Curriculares Nacionais (PCN), um documento que visa clarificar os objetivos da educação básica no país, nas mais diversas áreas do conhecimento escolar. Os PCN contam com um volume especial para a matemática e nele temos alusão à importância dos processos de argumentação e prova no ensino,

Se por um lado a prática da argumentação tem como contexto natural o plano das discussões, na qual se podem defender diferentes pontos de vista, por outro ela também pode ser um caminho que conduz à demonstração. Assim, é desejável que no terceiro ciclo se trabalhe para desenvolver a argumentação, de modo que os alunos não se satisfaçam apenas com a produção de respostas a afirmações, mas assumam a atitude de sempre tentar justificá-las. Tendo por base esse trabalho, pode- se avançar no quarto ciclo para que o aluno reconheça a importância das demonstrações em Matemática, compreendendo provas de alguns teoremas (BRASIL, 1998, p. 71-72).

Não é possível dizer que a publicação dos PCN impulsionou um trabalho com provas e demonstrações nas salas de aula. Ainda não há evidências para sustentar esta afirmação. Entretanto, por conta das exigências do Programa Nacional do Livro Didático (PNLD), algumas mudanças já podem ser percebidas neste tipo de material. Pais (2010) verificou uma mudança na abordagem dos livros didáticos das séries finais do ensino fundamental, constatando a presença de argumentações em geometria, mas demasiada valorização a conclusões derivadas do empirismo. Além disso, o pesquisador percebeu uma relação entre a argumentação e a resolução de problemas e um aumento da indução como estratégia de validação. Carvalho (2007) constatou que os livros didáticos do primeiro ano do ensino médio apresentam justificativas formais e informais às propriedades abordadas no campo algébrico, mas poucos propõem atividades para que os alunos, por si próprios, se engajem no processo de elaboração de provas.

A importância do processo de prova no ensino de matemática também gerou interesse nos pesquisadores brasileiros da Educação Matemática nestes últimos anos. Diversos estudos foram conduzidos nesta área na tentativa de (1) conhecer as concepções de estudantes e professores a respeito do que é uma prova, (2) compreender os entraves da utilização de uma abordagem voltada ao ensino de provas por professores, e (3) descrever as provas produzidas pelos alunos da educação básica e do ensino superior em termos das representações, generalidade e raciocínios utilizados.

Jahn e Healy (2008) mapearam as concepções sobre prova dos alunos da educação básica entre 14-16 anos de escolas do Estado de São Paulo. Este mapeamento revelou principalmente um baixo desempenho dos estudantes na elaboração de provas para conjecturas geométricas e algébricas. Leandro (2010), que participou do projeto das pesquisadoras, constatou que, para questões envolvendo os conceitos de fatorial, múltiplos e divisores, os acertos dos participantes foram diminuindo à medida que a possibilidade de realizar cálculos ficava inviável. A análise dimensional realizada apontou dois grupos de alunos: aqueles os quais utilizam o cálculo como principal estratégia para justificar suas afirmações e aqueles que utilizam propriedades. Estes últimos apareceram em menor quantidade. Piccelli e Bittar (2010) realizaram um experimento com alunos do ensino médio no contexto da geometria dinâmica e encontraram resultados similares. Grande parte das provas apresentadas pelos participantes foi desenvolvida com base em argumentos empíricos. As pesquisadoras apontaram que as explicações mais genéricas somente vieram à tona com a intervenção do professor ou quando alunos passaram a ficar mais familiarizados com a tarefa.

Freitas (2004) e Sales e Pais (2010) analisaram o processo de prova nos anos iniciais do curso de Licenciatura em Matemática. Segundo Freitas (2004) muitos estudantes apelaram para o empirismo como forma de argumentação. Entretanto, o pesquisador observou a presença considerável de argumentos mais genéricos redigidos em língua natural e algebricamente. Sales e Pais (2010) obtiveram resultados semelhantes. De acordo com ambos os estudos, grande parte das provas apresentadas pelos participantes não estava no formato aceito pela comunidade matemática, mas tinham grande potencial de progredir.

A partir de Reid e Knipping (2010) é possível perceber que os resultados das pesquisas internacionais no que tange à aprendizagem de prova são muito parecidos com os resultados brasileiros. De acordo com os pesquisadores, os estudos internacionais revelam que muitos estudantes,

(1) aceitam exemplos como forma de validação, (2) não aceitam provas dedutivas como forma de validação, (3) não aceitam contraexemplos como refutação, (4) aceitam provas dedutivas falhas como forma de validação, (5) aceitam argumentos sem coerência lógica, (6) oferecem argumentos empíricos como prova e (7) não conseguiriam redigir provas consistentes com os padrões da comunidade matemática (REID e KNIPPING, 2010, p. 59).

Os resultados de pesquisas discutidos anteriormente nos fornecem uma ideia de como anda a aprendizagem dos estudantes no que concerne ao processo de prova. De modo geral, é possível perceber que o desempenho dos mesmos é bastante limitado no que tange à compreensão e à elaboração de provas na matemática. Estes resultados podem ser interpretados e explicados por diferentes pontos de vista. Destaco alguns.

Pietropaoloet. al. (2009) analisaram a concepção de professores e pesquisadores sobre a necessidade de implementação de provas e demonstrações na educação básica. Os pesquisadores constataram que os professores pouco utilizam demonstrações em suas aulas por acreditarem que este é um discurso acessível para poucos alunos. Em contrapartida, quando se fala da prova de uma maneira mais flexível em termos de formalismos, os mesmos participantes admitem a possibilidade de um trabalho frutífero em sala de aula. Na mesma linha de pesquisa, Almouloud e Fusco (2010) analisaram depoimentos de professores da educação básica do estado de São Paulo e constataram que os mesmos trabalham pouco com demonstrações ao ensinarem equações quadráticas porque (1) não querem assustar os alunos, uma vez que os mesmos não têm base para entendê-las, (2) não possuem familiaridade com o ensino de demonstrações e (3) o livro didático não dá suporte a esse ensino. Ambos os estudos apontam a necessidade de se trabalhar a questão do ensino das provas e demonstrações nos cursos de formação inicial e continuada de professores levando-se em conta uma perspectiva mais flexível.

Balacheff (1999) aponta a existência de um contrato didático natural nas salas de aula da educação básica em que o professor assume a garantia da legitimidade e validade epistemológica do conceito que está sendo construído, de tal forma que o estudante é privado de um acesso autêntico à problemática da verdade e da prova. O pesquisador acredita que as dificuldades de ensino e aprendizagem de prova estão relacionadas a este contrato e que a superação dessas dificuldades reside na devolução ao estudante da responsabilidade matemática de suas produções, o que poderia ocorrer por meio de situações de interação social promovidas em sala de aula. Nesta mesma direção, Küchemann (2008) aponta que as dificuldades em provar estão relacionadas à falta de oportunidade dos estudantes se engajarem num processo de procura à estrutura inerente à determinada conjectura em sala de aula. Reid e Zack (2009) apontam sugestões e afirmam que três características podem ser combinadas a fim de favorecer o processo de prova: (1) colocar os estudantes numa situação de formulação de conjecturas, (2) deixar para eles a responsabilidade de formular um critério para avaliar as próprias respostas e as dos colegas, (3) colocar a comunicação dos resultados como uma das metas do processo.

Para Duval (2006) e Duval e Egret (1989) as dificuldades de aprendizagem de demonstrações estão relacionadas aos processos cognitivos demandados na sua formulação. Os pesquisadores acreditam que, para provar, os estudantes precisam estar conscientes dos diferentes significados das proposições usadas na dedução, e ainda, estar conscientes dos diferentes processos de organização exigidos na elaboração de uma prova: agrupar argumentos para formar uma cadeia dedutiva e agrupar cadeias dedutivas para formar uma prova. Para a superação destas dificuldades, ambos os estudos sugerem o uso de tarefas em sala de aula em que a representação não-discursiva da prova seja intercalada com representações em língua natural. Dois exemplos desse tipo de tarefas podem ser encontrados em Almouloud (2003, p. 137-138).

Na mesma linha das dificuldades cognitivas, Reid (2012) argumenta que o processo de produção de demonstrações é marcado por um sentimento de necessidade (feeling ofnecessity). O sentimento de necessidade também é apontado por Duval (2006) como um dos pré-requisitos para demonstrar. Este sentimento está relacionado à necessidade de explicar situações e fenômenos com argumentos não baseados na visualização e em acordos sociais. Ele é importante para o convencimento, uma vez que, neste contexto, as conclusões somente são alcançadas por meio de raciocínios baseados em afirmações anteriores das quais já temos certeza da validade.

Além das explicações para as dificuldades dos estudantes em compreender e redigir provas, ainda existe a possibilidade de reinterpretações dos resultados de pesquisa. Para o fato da maioria dos estudantes somente produzir provas empíricas, por exemplo, o estudo de Healy e Hoyles (2000) mostrou que grande parte dos participantes que construíram provas empíricas foi capaz de valorizar provas baseadas em argumentos genéricos e explicativos. Eles reconheceram que os argumentos construídos por eles não receberiam uma boa avaliação do professor. Apesar de notarem o poder dos argumentos algébricos, os participantes afirmaram que os exemplos particulares são meios poderosos de obter a convicção da verdade de uma afirmação, principalmente quando ela não é familiar.

Healy e Hoyles (2000) ainda afirmam que, embora as provas dos estudantes tenham sido pautadas em argumentos empíricos, muitos alunos apresentaram, em suas soluções, a estrutura: produção de evidências – descoberta de padrões – conferência de resultados. As pesquisadoras argumentam que essa abordagem está presente nas indicações curriculares que as escolas inglesas devem seguir. Com isso, os resultados desse estudo indicaram que o currículo estava influenciando a maneira como os estudantes apresentavam suas provas.

Outro resultado que pode ser reinterpretado é o fato dos estudantes precisarem de exemplos empíricos para confirmar uma conjectura mesmo depois de ela ter sido provada de forma genérica. Uma das explicações para tal atitude é dizer que os alunos não compreendem o poder generalizador de uma prova. Entretanto, Küchemann e Hoyles (2009) perceberam que, em muitos casos, os alunos fazem apelo a testes numéricos depois de uma prova para checar a validade da estrutura do argumento que eles construíram e para aumentar a confiança nas suas produções. Hanna (2000) ainda afirma que, para muitos estudantes, o papel da prova tem o mesmo significado que para os cientistas experimentais, como os físicos. Para estes, a prova precisa ser acrescida de exemplos práticos para ter sentido. Neste contexto, o desafio para os educadores seria levar os estudantes a mesclarem dedução e experimentação, relacionando matemática e o mundo real.

Todos estes resultados de pesquisa me fizeram buscar novas direções para o ensino de provas na escola, uma vez que esta é uma atividade que caracteriza o conhecimento matemático. Nas próximas seções, mostrarei como atividades realizadas no computador podem fazer com que estudantes formulem suas próprias conjecturas, no campo geométrico e algébrico, e tenham curiosidade de buscar explicações conceituais e formais para as mesmas.

O PAPEL DO COMPUTADOR NO PROCESSO DE FORMULAÇÃO DE CONJECTURAS

Conjecturar é o mesmo que formular uma hipótese. Neste sentido,a conjectura pode ser vista comouma afirmação generalizadora que requer verificações adicionais(REID & KNIPPING, 2010, p. 91-92).
A formulação de uma conjectura depende da realização de testes sistemáticos e da percepção de regularidades numa determinada situação. É neste contexto de exploração de padrões matemáticos que o computador pode ser integrado às atividades do estudante de modo significativo.A seguir, discutirei como dois ambientes computacionais, o CabriGéomètre e o Consecutivo, podem ser utilizados a fim de contribuir com o processo de formulação de conjecturas na geometria e na álgebra, respectivamente.

O Cabri-Géomètre, ou simplesmente Cabri, é um softwareo qual permite aos estudantes de todos os níveis escolares a construção e manipulação dinâmica de formas geométricas planas. A primeira versão do programa foi desenvolvida na França, em 1986, por um grupo de pesquisas em Educação Matemática, liderado por Jean-Marie Laborde. No Brasil, o Cabri é comercializado desde 1992 e já esteve no centro de diversas pesquisas envolvendo o ensino e aprendizagem de Geometria. Outros softwares com o mesmo propósito já foram desenvolvidos, como é o caso do Geometer’sSketchpad e do Geogebra. Programas como estes, são conhecidos no cenário educacional internacional com Ambientes de Geometria Dinâmica (ADG) e têm provocado mudanças nas relações dos estudantes com o conhecimento geométrico.

No ambiente do Cabri é possível encontrar ferramentas as quais fomentam o aparecimento de práticas importantes para a formulação de conjecturas. Centralizarei minhas discussões em duas destas ferramentas: o arrastar e o medir.

Ao se construir um objeto na tela do Cabri é possível movimentá-lo de diversas maneiras, utilizando-se a ferramenta arrastar. Um quadrilátero ABCD, por exemplo, pode assumir diversas formas como mostra a Figura 1 e a Figura 2

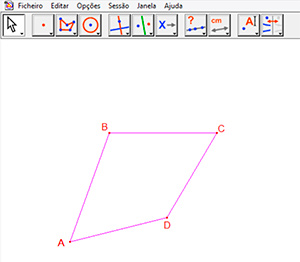
Figura 1: Quadrilátero ABCD no Cabri.

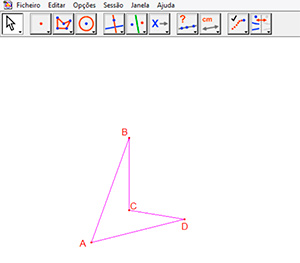
Figura 2: Quadrilátero ABCD no Cabri após o movimento do vértice C.

Os professores podem pedir a um estudante que construa um quadrilátero ABCD, marque os pontos médios de seus lados e construa um novo quadrilátero MNPQ por estes pontos médios. Ao arrastar esta construção, o estudante verá que o quadrilátero MNPQ continua ligado aos pontos médios dos lados do quadrilátero ABCD independentemente do movimento que se faça na tela (Figura 3 e Figura 4).

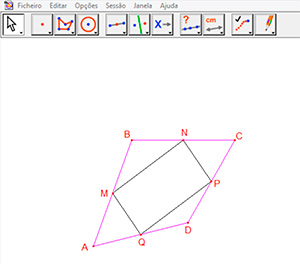
Figura 3: Quadrilátero MNPQ no Cabri.

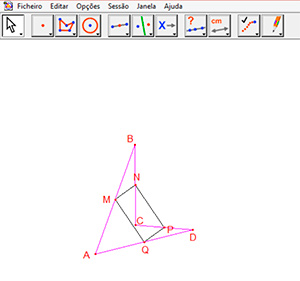
Figura 4: Quadrilátero MNPQ no Cabri após o movimento do vértice C.

Para incentivar a formulação de conjecturas, o professor pode pedir que o estudante explore o quadrilátero MNPQ para seja descoberta a natureza do mesmo. Esta exploração pode ser realizada com o uso da ferramenta medir. Com ela, o estudante pode determinar as medidas dos lados e dos ângulos internos do quadrilátero em questão(Figura 5 e Figura 6).

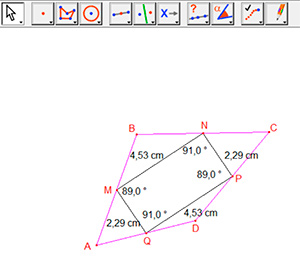
Figura 5: Quadrilátero MNPQ com medidas de lados e ângulos internos.

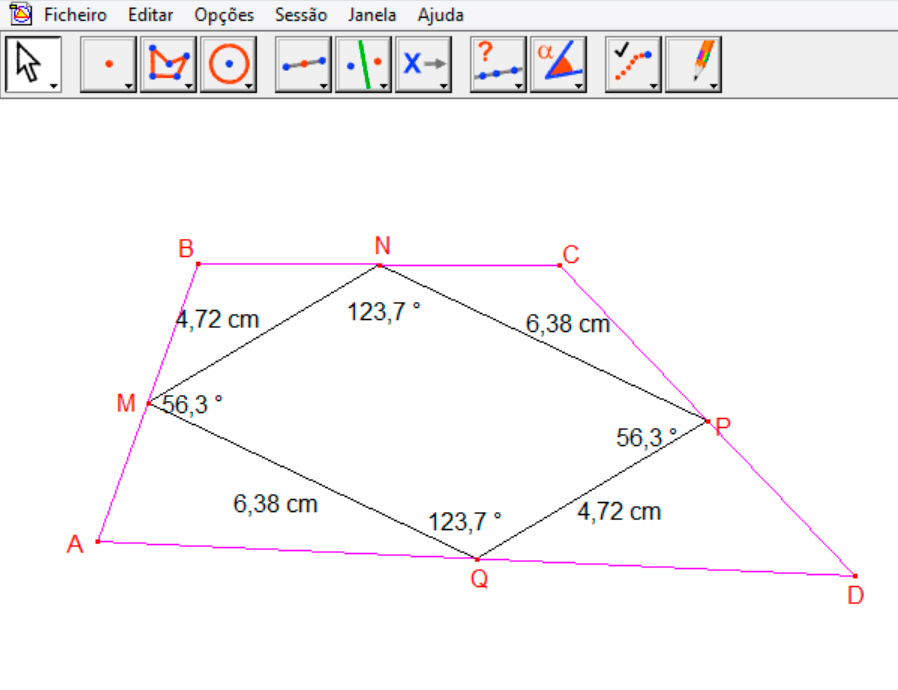
Figura 6: Quadrilátero MNPQ com medidas de lados e ângulos internos após o movimento dos vértices C e D.

Depois das medições, ao arrastar a construção na tela, o estudante notará que todas as medidas aferidas se alteram com o movimento, mas que o quadrilátero mantém suas características iniciais. O movimento da figura associado à observação sistemática de suas medidas pode levar o estudante a perceber que os lados opostos do quadrilátero MNPQ são congruentes, assim como os ângulos internos opostos. Esta percepção pode fazer com que o aluno conjecture que o quadrilátero MNPQ é um paralelogramo.

Apesar de mais comum, a possibilidade de utilizar o computador para auxiliar o estudante no processo de formulação de conjecturas vai além do campo geométrico. Há também muitos softwares dinâmicos que podem fomentar a percepção de regularidades numéricas e algébricas. Um exemplo deles é o Consecutivo, software que eu mesma desenvolvi como parte do meu projeto de doutorado.
O Consecutivo possui diversas ferramentas as quais podem auxiliar os estudantes a formular conjecturas a respeito da soma e do produto de uma sequência de números consecutivos. Neste texto,discutirei três destas ferramentas: as barras de rolagem, a reta numérica e a caixa de soma. Para ilustrar como estas ferramentas contribuem para a formulação de conjecturas, apresentarei as produções de uma dupla de estudantes a qual participou de uma das aplicações do programa em escolas.

Aos estudantes do segundo ano do ensino médio de uma escola pública do estado de São Paulo foi solicitada a utilizaçãodo Consecutivo para investigar regularidades na soma de quatro números consecutivos. Uma dupla de participantes apresentou no papel a seguinte conjectura:

Figura 7: Conjectura formulada por estudantes com o auxílio do Consecutivo.

Ao assistir aos vídeos com as interações da dupla enquanto a mesma lidava com o programa, observei que os participantes chegaram a esta conclusão manipulando as ferramentas na tela da seguinte maneira: (1) a dupla posicionou uma das barras de rolagem no valor quatro, uma vez que era solicitado que se investigasse a soma de quatro número consecutivos, (2) um dos participantes começou a movimentar a segunda barra de rolagem alterando o valor do primeiro número da sequência de consecutivos e (3) enquanto movimentavam a segunda barra de rolagem, os dois participantes observavam as variações dos resultados da soma e do primeiro número da sequência na reta numérica (Figura 8).

O dinamismo com o qual os valores se alteravam na tela do computador possibilitou aos estudantes a percepção de regularidades, que ficavam cada vez mais evidentes conforme os estudantes realizavam mais testes dentro do domínio que eles desejavam. Neste caso, os movimentos das barras associados à observação dos resultados da soma fizeram com que os participantes concluíssem que a soma de quatro números consecutivos aumenta de quatro em quatro unidades toda vez que se aumenta uma unidade no primeiro número da sequência. Como a primeira soma, que eles puderam encontrar, resultava em seis, eles conjecturaram que a soma de quatro números consecutivos corresponde a quatro vezes o primeiro número da sequência mais seis.

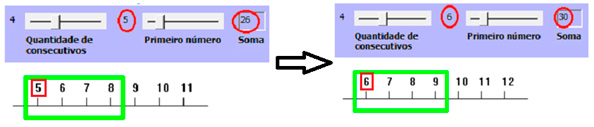
Figura 8: Ações dos estudantes no Consecutivo.

Mesmo com objetivos diferentes, o Cabri e o Consecutivo possuem ferramentas importantes quando se deseja perceber padrões matemáticos e elaborar conjecturas. No Cabri, a ferramenta medir coloca na tela do estudante elementos para serem observados e a ferramenta arrastar permite que essas observações ocorram de forma sistemática até que se perceba uma invariância. No Consecutivo, de forma análoga, as ferramentas caixa de soma e reta numérica colocam os valores na tela. A ferramenta barra de rolagem permite que estes valores sejam alterados de forma sistemática até que se perceba uma regularidade.

Muitos pesquisadores já discutiram sobre as potencialidades dos softwares para a formulação de conjecturas. Hoyles (2012), por exemplo, afirma que,

As tecnologias digitais podem fornecer ferramentas que são dinâmicas, gráficas e interativas. Mais do que isto, elas podem dar suporte a processos de criação e exploração de conjecturas, uma vez que elas oferecem ao estudante a possibilidade de transitar entre o dinâmico e o estático, o que dá aos aprendizes um controle reflexivo (HOYLES, 2012, p. 4).

Nesta mesma linha de pensamento, Moreno-Armella, HegeduseKaput (2008, p. 12) salientam que “as ferramentas tecnológicas digitais permitem os estudantes perceber e generalizar estruturas matemática por meio de colaboração co-ativa com o ambiente”.

O PAPEL DO COMPUTADOR NO PROCESSO DE FORMULAÇÃO DE JUSTIFICATIVAS FORMAIS

Na seção anterior, discuti como o computador pode contribuir para que o estudante perceba padrões matemáticos e formule conjecturas. Contudo, é possível utilizar o computador para ir mais além. É possível utilizá-lo para ajudar o estudante a validar suas hipóteses e a compreender porque as mesmas são verdadeiras e fazem sentido.

Na situação envolvendo o softwareCabri, o quadrilátero MNPQ é um paralelogramo. O estudante pode se convencer da validade desta conjectura facilmente, pois ao movimentar os vértices do quadrilátero ABCD de várias maneiras perceberá que os lados e ângulos opostos do quadrilátero MNPQ continuam sempre congruentes. Neste contexto, pode-se falar em teorema situado e prova situada (MORENO-ARMELLA e SRIRAMAN, 2005). Isto quer dizer que as conjecturas formuladas dentro do ambiente computacional ganham força de teorema rapidamente para o aluno, uma vez que o mesmo observa na tela que as propriedades em questão se mantêm rígidas para uma infinidade de casos obtidos com o movimento da figura. Entretanto, é possível utilizar o computador para ir além das provas situadas se considerarmos que a prova é mais do que um conjunto de argumentos convencedores. A prova é uma explicação a qual pode dar sentido à conjectura e mostrar ao estudante as razões de sua origem.

Na situação do Cabri, esta prova pode ser obtida se os estudantes acrescentarem novos elementos à figura que está na tela. Se eles construírem e medirem a diagonal AC do quadrilátero ABCD, perceberão que essa diagonal é paralela aos segmentos MN e PQ e que possui o dobro de seus tamanhos. Isto porque o triângulo ABC é semelhante ao triângulo MBN e o triângulo ADC é semelhante ao triângulo QDP (Figura 9).

Se o estudante souber que se dois segmentos de reta são paralelos a um terceiro, eles são paralelos entre si, eles podem concluir que os lados MN e PQ do quadrilátero MNPQ são paralelos. Fazendo-se o mesmo procedimento ao traçar a diagonal BD do quadrilátero ABCD, explica-se porque os lados MQ e NP também são paralelos. Estas duas conclusões completariam a prova de que o quadrilátero MNPQ é um paralelogramo.

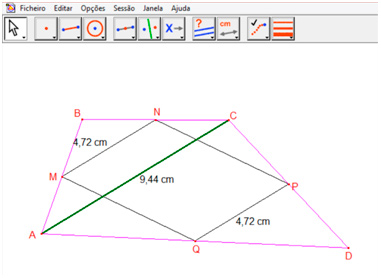
Figura 9: Quadrilátero ABCD com a diagonal AC traçada.

Também é possível utilizar as ferramentas do Consecutivo para criar uma prova. A seguir analiso a explicação dada pela dupla que formulou a conjectura a respeito da soma de quatro números consecutivos(Figura 10).

Figura 10: Prova apresentada pelos estudantes ao interagirem com o Consecutivo

Ao analisar os vídeos com as interações desses participantes, verifiquei que os mesmos perceberam que a cada mudança de unidade na barra de rolagem, uma unidade era acrescentada a cada número da sequência de consecutivos. Como estes números seriam somados ao final do movimento, a nova soma corresponderia a quatro unidades a mais do que a soma anterior. Veja um esquema da interação dos estudantes na Figura 11.

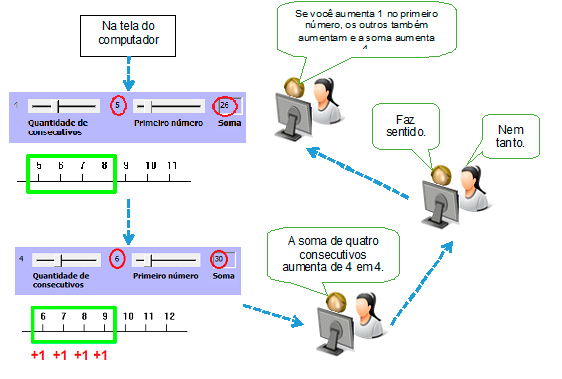
Figura 11: Interação dos participantes ao elaborarem uma prova no Consecutivo.

Ao perceberem novas propriedades, os participantes explicaram para eles mesmos porque a conjectura que eles formularam fazia sentido, o que reforçou ainda mais a confiança na mesma.

A possibilidade de dar novos significados à prova na escola já foi discutida por muitos pesquisadores. Hanna (2000) afirma que a prova pode ser utilizada em sala de aula como mais uma forma de trazer compreensão às situações matemáticas. De Villiers (2001) salienta que a prova pode ser um instrumento validação, explicação e também de desafio intelectual. Sinclair e Robutti (2013) reconhecem que o uso de ambientes dinâmicos pode ajudar os estudantes a transitar do campo espacial-gráfico para o campo teórico no que diz respeito aos conceitos de geometria, o que auxiliaria no processo de prova de conjecturas. Healy (2000) mostrou que as interações entre o estudante e o computador fazem emergir a conjectura e a prova simultaneamente, uma vez que o uso de exemplos genéricos e casos especiais formam a base dos argumentos formulados por estudantes nestes ambientes.

CONSIDERAÇÕES FINAIS

Neste artigo, dissertei a respeito do trabalho com a formulação de conjecturas e justificativas formais no ambiente escolar, enfatizando que práticas como estas, apesar de caracterizarem a Matemática como ciência, têm sido negligenciadas nas salas de aulas brasileiras nas últimas décadas. Na tentativa de resgatar tais práticas, apresentei duas sugestões em que o computador aparece como uma ferramenta com potencial para encorajar nossos estudantes a perceber regularidades e explicar porque elas ocorrem. Mas por que os computadores possuem este potencial? Quais são as potencialidades e limitações de um ensino que tem o computador integrado a sua rotina? Compartilharei com o leitor algumas respostas pessoais para tais questionamentos.

As ferramentas computacionais nas últimas três décadas se tornaram portáteis, poderosas e de custo acessível ao cidadão comum. A internet teve seu uso disseminado de tal forma que a possibilidade de se conectar em tempo real com diversas pessoas em lugares diferentes já não é mais coisa de filme de ficção científica. As mudanças também estão presentes em nossas salas de aula. Hoje, grande parte das escolas brasileiras possui computadores disponíveis aos estudantes e nossas salas de aula estão repletas de alunos com celulares e dispositivos portáteis diversificados. Esta evolução não ocorreu somente na escala do hardware. Softwares e aplicativos de cunho educacional dos mais variados são lançados diariamente no mercado brasileiro e internacional.

Dos anos 80 até o presente,há muitos programas de computador os quais podem contribuir significativamente com o processo de ensino e aprendizagem de Matemática. É o caso do CabriGéomètre e do Consecutivo, abordados nas seções anteriores deste texto. Estes programas possuem características importantes capazes de fazer com que os estudantes percebam e expliquem padrões matemáticos. Duas destas características foram destacadas neste artigo. A primeira delas é a presença de ferramentas que possibilitam o movimento de objetos na tela do computador sem que as propriedades dos mesmos sejam destruídas durante essa movimentação. A segunda é a possibilidade de medição de ângulos e comprimentos e o cálculo automático de somas e diferenças.

Quando os estudantes articulam os resultados de medições e cálculos com a mudança dinâmica destes elementos na tela do computador, eles se engajam numa atividade de observação sistemática que converge, em muitas ocasiões, para a percepção de invariâncias. São estas invariâncias que dão origem às conjecturas. Além disso, a exploração dos esquemas construídos na tela do computador também tem o potencial de fazer emergir justificativas para as conjecturas formuladas, uma vez que os movimentos e observações podem resultar na percepção de propriedades inerentes à situação que está sendo representada na tela do computador.

Apesar das contribuições que o computador pode trazer para a educação, a integração do mesmo à rotina escolar ainda é tímida noque diz respeito o processo de ensino e aprendizagem de matemática. Muitos fatores contribuem para esta situação. Cito três deles.

Primeiramente, quando a rotina de sala de aula começa a extrapolar o tradicionalismo de um ensino centrado na figura do professor, estudantes, pais e a sociedade, de forma geral, podem apresentar atitudes e questionamentos desfavoráveis, principalmente no que se refere ao uso de tecnologias como calculadoras e computadores nas aulas de matemática. O pensamento mais comum é o seguinte: “se o computador vai realizar os cálculos e medições, qual será o trabalho do aluno?”. Este tipo de questionamento geralmente está associado a uma visão limitada sobre o que consiste a atividade matemática. Esta atividade vai muito além das operações com números e equações. A Matemática também é a ciência dos padrões, regularidades e das explicações logicamente conectadas; é principalmente para esta Matemática que o computador revela sua importância em sala de aula.

O segundo fator tem relação com a integração das tecnologias ao currículo e ao sistema de avaliação da aprendizagem. Atualmente, grande parte do currículo de matemática é baseada em conceitos e representações dependentes do ambiente estático do papel e lápis. Além disso, as avaliações são desenhadas para contemplar as características deste tipo de currículo. Então, quando o professor decide utilizar outros recursos em sala de aula, estas práticas parecem desconectadas de suas ações rotineiras. É como se os professores precisassem “parar” os conteúdos toda vez que decidirem utilizar tecnologias em sala de aula. Apesar dos avanços nas pesquisas em Educação Matemática, que valorizam as tecnologias, e da corrida das editoras para a reformulação de materiais didáticos que conectem tecnologia e conteúdos disciplinares, sinto falta de uma integração significativa das tecnologias digitais ao currículo e ao sistema de avaliação.

O terceiro fator diz respeito às atitudes do professor de matemática frente às tecnologias. Utilizar o computador de forma significativa em sala de aula requer uma alteração no contrato didático entre professor e aluno. A aula passa a ser centrada naquilo que os alunos podem descobrir ao interagirem com o computador e calculadoras. Neste contexto, muitos conceitos e explicações diferentes podem emergir. Esta variedade tira o professor de sua “zona de conforto” e traz para a sala de aula uma movimentação diferente daquela com a qual estão acostumados. Além disso, o uso significativo das tecnologias digitais nas aulas de matemática exige que o professor pesquise situações e problemáticas em que as mesmas sejam indispensáveis e façam a diferença em relação ao ambiente do papel e lápis. Isto requer uma atitude de aprimoramento contínuo do professor como profissional.

Acredito que os três fatores discutidos anteriormente sejam entraves superáveis com ações em duas dimensões. Na primeira dimensão, há necessidade de implementação de políticas públicas que visem à reformulação do currículo, do sistema de avaliação e que se preocupem com a formação contínua do professor de matemática. Na segunda dimensão, é preciso fazer chegar às salas de aulas as mais diversas sugestões e inovações propostas nas pesquisas em Educação Matemática. Este artigo foi uma tentativa de contribuição para este segundo caso.

REFERÊNCIAS

1. Para a Matemática, um teorema é uma conjectura que foi provada formalmente.

ALMOULOUD, S. A. Registros de representação semiótica e compreensão de conceitos geométricos. In: S. D. A. Machado (Org.). Aprendizagem em matemática: registros de representação semiótica. Campinas: Papirus, 2003. p. 125 – 147.
______; FUSCO, C.A.S. Provas e demonstrações em matemática: uma questão problemática nas práticas docentes no ensino básico. In:ENCONTRO NACIONAL DE EDUCAÇÃO MATEMÁTICA, 10., 2010, Salvador, BA. Anais…Disponível em: . Acesso: em 23 set. 2013.

BALACHEFF, N. Is an argumentation an obstacle? Invitation to a debate… International Newsletter on the Teaching and Learning of Mathematical proof. maio/jun. 1999.Disponívelem: . Acesso em: 23 set. 2013.

BRASIL. Secretaria da Educação Fundamental. Parâmetros Curriculares Nacionais: terceiro e quarto ciclos do ensino fundamental: Matemática.Brasília: MEC/SEF, 1998.

CARVALHO, C. C. S. Uma análise praxeológica das tarefas de prova e demonstração em tópicos de álgebra abordados no primeiro ano do ensino médio. Dissertação (Mestrado em Educação Matemática)- Pontifícia Universidade Católica de São Paulo, São Paulo, 2007.

DE VILLIERS, M. Papel e funções da demonstração no trabalho com o Sketchpad. Educação e Matemática. n. 62, p. 31-36, maio/jun. 2001.

DUVAL, R. Cognitive functioning and the understanding of mahtematical process of proof. In: BOERO, P. (Org.).Theorems in school: from history, epistemology and cognition to classroom practice. Rotterdam: Sense Publishers, 2006. p. 137–162.

______; EGRET, M. A. L’organisation deductive du discours: Interaction entre structure profondeet structure de surface dansl’accès à la démonstration. Annales de Ditactique et de SciencesCognitives. Strasbourg,1989. v. 2, p. 25-40.
FREITAS, J. L. M. Produção de provas em aritmética-álgebra por alunos iniciantes da licenciatura em matemática. In: ENCONTRO NACIONAL DE EDUCAÇÃO MATEMÁTICA, 8., 2004, Recife, PE.Anais… Recife, PE, 2004. p. 1–13. Disponível em: . Acessoem: 23 de set. 2013.

HANNA, G. Proof, explanation and exploration: an overview. Educational studies in mathematics, v. 44, n. 1, p. 5–23, 2000.

HEALY, L. Blurring distinction between the empirical and the theoretical?The roles of examples in the proving process. EducaçãoMatemáticaPesquisa, v. 2, p. 51–63,2000.

______ ;HOYLES, C. A study of proof conceptions in algebra. Journal for Research in Mathematics Education, v. 31, n. 4, p. 396–428, jul. 2000.

HOYLES, C. Tackling the mathematics: potential and challenges for research in mathematics education. In: SEMINÁRIO INTERNACIONAL DE PESQUISA EM EDUCAÇÃO MATEMÁTICA, 5., 2012,Petrópolis.Anais…Petrópolis,RJ, 2012. p. 1–11. Disponível em: Acesso em: 23 set. 2013.

JAHN, A. P. ;HEALY, L. Argumentação e prova na sala de aula de matemática: design colaborativo de cenários de aprendizagem. In: REUNIÃO ANUAL DA ASSOCIAÇÃO NACIONAL DE PÓS-GRADUAÇÃO E PESQUISA EM EDUCAÇÃO, 31., 2008, Caxambu, MG. Anais….Caxambu, MG, 2008.

KÜCHEMANN, D. E. Looking for structure: areport of the proof materials project.London: Dexter, 2008.

______;HOYLES, C. From empirical to structural reasoning in mathematics: tracking changes over time. In:DESPINA, A. et al.(Ed.).Teaching and learning proof across the grades: a K-16 perspective. New York: Routledge, 2009. p. 171–190.

LEANDRO, E. J. Argumentação e provas matemáticas: desempenho de estudantes brasileiros com idade entre 14 e 16 anos. In:ENCONTRO NACIONAL DE EDUCAÇÃO MATEMÁTICA, 10., 2010, Salvador, BA. Anais…Salvador/BA, 2010. p. 1–12.

MORENO-ARMELLA, L. ;SRIRAMAN, B. Structural stability and dynamic geometry: some ideas on situated proofs. ZDM: Analyses, Springer-Verlarg, v. 37, n. 3, p. 1–10, 2005.

______ ; HEGEDUS, S. J. ;KAPUT, J. J. From static to dynamic mathematics: Historical and representational perspectives. EducationalStudies in Mathematics.n.68,p. 99–111, 2008.

PAIS, L. C. Argumentação no estudo da geometria nos anos finais do ensino fundamental: livros didáticos e formação de professores. In: ENCONTRO NACIONAL DE EDUCAÇÃO MATEMÁTICA, 10., 2010, Salvador, BA. Anais… Salvador/BA, 2010. p. 1–19.

PICCELLI, P. H. ; BITTAR, M. A validação de conjecturas como parte do processo de ensino e aprendizagem da matemática. In: ENCONTRO NACIONAL DE EDUCAÇÃO MATEMÁTICA, 10., 2010. Salvador, BA.Anais…Salvador/BA, 2010. p. 1–9.

PIETROPAOLO, R. C. et. al. Concepções sobre demonstrações e provas nos currículos da formação inicial de professores de matemática. In: SEMINÀRIO INTERNACIONAL DE PESQUISA EM EDUCAÇÃO MATEMÁTICA, 4., 2009, Brasília, DF. Anais… Brasília, 2009. p. 1–19.

REID, D. A. Biological bases for deductive reasoning. CONFERENCE OF THE EUROPEAN SOCIETY FOR RESEARCH IN MATHEMATICS EDUCATION, 8th.,2012. Side-Antalya, TU. Anais…Side-Antalya, Turkey, 2012. p. 1–10. Disponível em: Acesso: em 26 mar. 2013.

______;ZACK, V. Aspects of teaching proving in upper elementary school. In:DESPINA A. et al. (Ed.). Teaching and learning proof across the grades: a K-16 perspective. New York: Routledge, 2009. p. 133–146.

______; KNIPPING, C. Proof in Mathematics Education: research, learning and teaching.Rotterdam:SensePublishers, 2010.

SALES, A.; PAIS, L. C. Argumentação e demonstração em uma atividade de geometria em um curso de licenciatura em matemática. In: ENCONTRO NACIONAL DE EDUCAÇÃO MATEMÀTICA, 10., 2010, Salvador, BA.Anais… Salvador/BA. 2010. p. 1–11.

SINCLAIR, N.; ROBUTTI, O. Technology and the role of proof: the case of dynamic geometry. In:CLEMENTS, M. A. et. al. (Ed.), Third International Handbook of Mathematics Education. New York: Springer, 2013. p. 571-596.